HexLife postmortem

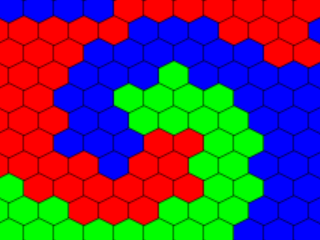
 As the GameDev.tv Game Jam gives participants a free course, I figured I had to do something with this Jam. The theme of the jam was “Life in 2 Dimensions” so my immediate thought came to Conway’s game of Life. Life is a cellular automata simulator with a set of very simple rules for running that results in surprising results. My first change was to place the automata on a hex grid. I then added three types of life and set the rules so Red cells eat Green cells which eat Blue cells which eat Red cells. My idea was that I would have levels where you would place cells in such a way that your color would dominate the board.  I also made the decision to write the game entirely from scratch. 

What Went Right

The actual simulation aspect game together quickly and my preliminary test showed that it worked producing a rather interesting swirling effect. While the simulation is fun to play with for short bursts, and random mode makes rather interesting displays, by itself it is not really a game. My idea for a game was to have the player control one of the colors and attempt to turn the board entirely that color.  This, will be discussed in the what went wrong section.

Mixed Blessings

The decision to do the game from scratch was a good one considering I am planning to build a game engine from scratch so this would be good practice. I had not anticipated as much interruption from the real world as there was but it was good practice getting back to building everything. Had I gone with my own libraries, I would have been able to do a bit more polish on the game but as things stand it doesn’t look too bad the way that it is. While eating up a bit more time than I would have liked, creating the UI from scratch let me play around with different, and better, techniques than I have in my rather dated and overly simple SLL libraries. This will be helpful as I get further along in the book series I am working on.

What Went Wrong

While the sim as it stands has nice flashy displays, it is not quite enough to allow for good strategic design. I am sure that there are additional features and rules that could be added to allow for more strategy allowing for a challenging game, but that is not here. Unfortunately, the way the rules work make for a fairly easy way for finding solutions to win the game. I am undecided if I will revisit this game but with more rules and other features to increase the challenge of the game but that is certainly a possibility.

Final thoughts

I have been reneging on this blog, so I am thinking about taking my code for the game and cleaning it up going over the code and what I am doing to improve it. This would also result in some soapbox posts about a variety of topics. I'm not sure how often I am going to update this but may go to a fortnight format where I update  my book on Spelchan.com in one week and then post about my refactoring on this blog. I may also consider entering more game jams, depending on what my schedule is going to be like.

HexLife Beta

This is it for today and I am not sure how much time I will have Sunday and Monday, probably just Monday morning. The beta is on Spelchan.com, but there is a lot of work that needs to be done. What I want to get done before Monday’s deadline:

• More levels, as a single simple test level is not much of a campaign.
• Better title screen
• Instruction screen

What I hope to get done by Monday:

• Transition animation between generations.
• Ability to save and load levels.

What I will do after Monday’s deadline:

• Write a postmortem.
• Clean up the code. Right now, pretty smelly as I fell into the time pressure trap.

Possibly spend a few weeks going over my code (not sure if this would be here or on Spelchan.com). 

Hex Life Editor update

 I forgot how much work creating a GUI from scratch was. This is why libraries are nice but I am doing this from scratch. I now have an editor but still need to add a way of taking the edited levels and playing them as well as set goals for a level and a partial editor that lets the player place their color of cells on the board. 

Early build of editor mode for my HexLife game

My thoughts are that the goal will be to give the player an existing layout sans their color, and they need to strategically place their color in such a way that their color will end up taking over the entire board. I am not sure I will have much time at all tomorrow to work on this, but should be able to release a version of the editor and player Saturday. This would leave Sunday and Monday to create a set of levels and fine tune things.

Let there be Life

 When I said I was going to program the game from scratch, I wasn’t kidding. As I am trying to move back to test driven development, as I believe the AI world of programming will become more natural language programming with the responsibility of the programmers to make sure that what the natural language produces actually works properly so creating and testing programs will become a vital skill for the future of programming. I don’t think programmers will be going away, but their roles will be more focused on design, testing, security, and optimization. Still, using a testing framework would be third party, so I wrote my own simple testing framework (when I post the final version the tests will be included).

Writing automated tests seems to be slow, but I notice that I find bugs much quicker and am a bit more confident that my code does what it is supposed to. My tests are not as thorough as they should be but good enough for the scope of the project I am working on.

When creating the game, I realized my idea of moving cells was very problematic, so opted for a growing effect with the eating of cells being a predominant feature. Text versions seemed to work so I bit the bullet and created a graphical version (manually tested as graphics/GUIs are way too painful to automate, and if the underlying code it calls is tested there shouldn’t be a problem).

The simulation was automated and just generating random grids results in really cool results. The first phase has been posted so Thursday I will be focusing on creating an editor and the weekend on putting together a short campaign where you will be given a map and need to place your cells in such a way that they will take over the map. Something has come up for Wednesday, so while I might get an hour or two in, it is likely not going to be very much. Hopefully I will have something Thursday night to show, as Friday is busy. Why everything comes up when I want to do a Game Jam is annoying, but it is what it is.

The first build is available at https://spelchan.com/games/y2023/HexLife/index.php

See you Thursday???

GameDevTV Jam 2023 Planning

 It has been a while since I have posted something here, but now that I have a tiny bit of time, I can finally work on my own things, so am entering the GameDevTV jam for this year. Why? Everyone who enters gets a free course so why not? I am going to be focusing my free time on writing some books on creating a game engine from scratch, so in preparation for the game jam I will spend the days I am able to work on it creating a game from scratch. Unfortunately, I still do have other obligations so will only be able to get in 30-50 hours during the 10 days so will have to take that into account. I am losing this first weekend and next Friday for sure and suspect there will be interruptions on other days so we will see how much I am able to do.

What do I mean by from scratch? There will be no libraries or frameworks other than the standard libraries and what DOM provides. I will write all the code. Ideally,I will extend this restriction to artwork and sound effects but that will depend on how much time I have at the end for polishing the game.

The theme of the game is Life in 2 Dimensions. The thoughtI immediately came up with is some variation on Conway’s Game of Life (CGL). Doing a straight CGL would not be much of a challenge, but if I did this more like a strategy game then there could be something interesting.

My idea is to use a hex grid where there would be 3 distinct types of cells which are either food or enemies. Red Cells eat Green cells which eat Blue cells which eat Red cells. Each round is broken into phases. Phase 1 would be the absorption phase where the cells around each cell is counted. If there are more enemy cells touching a cell then allies, the cell will be absorbed becoming an enemy cell otherwise it stays the same. The next phase is the movement phase.  

The rules for movement are easy. Head towards the nearest food cell (or, fake food cell when I add that later) though only using empty cells, so will stay still if cells closer to food are currently blocked.  Not sure what order the cells will move in, will be playing around with that aspect. 

The game will be an attempt to convert the entire board to your color. With the ability to place fake food on the board to guide the activity. I am hoping to have a crude version of the game by Tuesday or Wednesday as due to other obligations I am not going to be able to start until Monday. 

The future comes from the past

 It has been a long time since I took a break from working on my 2600 emulator. Next month I am going to return to that project. Things have changed a lot since I worked on that project so have a lot of decisions to make. Web Assembly has become a real thing and there are several good paths to using it. Kotlin is not one of them. I am trying to decide if I should port to C, or Assembly Script. I am also thinking of going with an IDE instead of just an emulator. 

The next few months will be looking at tools and technology available followed by porting my existing emulator code. From there will be a matter of finishing the emulator then possibly building an IDE around things.

An Awful Month and a Postponed Decision

 Last month was rough and I am just getting caught up to where I should be this weekend. I am now working as a full-time college professor, which is a surprising amount of work. Making matters tricky was that just after finalizing the contract a major event happened.

My father passed away on August 20^th. He had been taken to the hospital a few days earlier for pneumonia. He had recovered from it and had been moved up to the rehabilitation floor. I was assuming he would only be there a couple of weeks before my caretaking duties would start again. Instead, as I was packing up the stuff he wanted me to bring him for my morning visit I got a phone call from the hospital with the bad news.

It is really strange when something like this happens as part of my mind knew he was gone but another part insisted that this was some type of prank or a mistake. I knew I was not in a proper mental state so asked my neighbor to drive me to the hospital. I simply had to verify that this was real with my own eyes. Stupid, perhaps, but at least I got to say goodbye to him.

Next was the funeral. Dad wanted just a small gathering of his closest friends and family. Thankfully my sisters were there to help prepare this as I had so much preparation to do in a short time. I did write the eulogy which took multiple attempts. I was warned that when giving a eulogy that you should do several dry runs so you can get through it without breaking down. I am glad I followed this advice. Even then, there were a few moments where I could hear my voice breaking and had to pause for a few seconds. What is interesting is that it was at the strangest moments. How hard of a worker he was. How much he cared for my mother. Even writing this I am struggling.

If this wasn’t bad enough to deal with, on the day of the funeral the air conditioner wasn’t clicking on and we had a plumbing issue. The plumbing was easily resolved, thankfully. The air conditioner, was also easy but had a warm house all that day as we simply didn’t have the time to look into the problem. It turns out that there is a switch to the furnace outside the furnace room that magically turned itself off. My nieces and nephews swear they never played with the switch and it is high enough on the wall  (above head height) to prevent accidentally turning it off.

Even after the funeral, I have lots of work to do, but spread out over a few months until probate is finished. Slowly packing things up is not hard work, but often results in surprising memories. Which finally leads to the point of this posting. I still have no idea what I am going to be doing with the site and blog so will be delaying my decision until next month.